Conservación de la energía (dentro de un calorímetro)

PDF

Si hasta hacia cuestión de un año atrás, había material que se usaba poco, o más bien nada, era el que se muestra más abajo.

Lo que se explica por el hecho de que, el programa de Física de 5to año del plan 2006 era (y sigue siendo en el nocturno) inabarcable, y Termodinámica quedaba con suerte en "agua borraja". En el plan vigente de 6to (3ro EMS), es posible usar, con modificaciones, ese material, tal como se muestra a continuación.

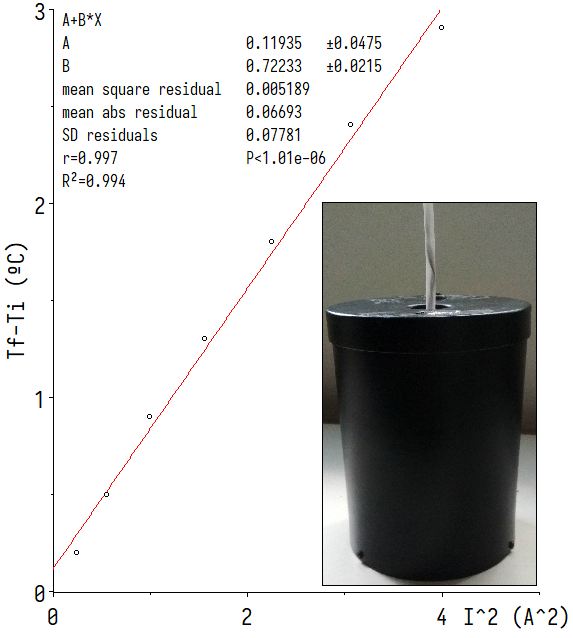
El calentador "original" es sustituido por este otro casero que se muestra a la derecha, y se mejora la aislación térmica de la tapa del calorímetro con ese tipo de espuma-plast, que no es telgopor, y que no sé como se llama. ¿Por qué las adaptaciones? Porque el calentador original no sirve, o al menos con la fuente de voltaje utilizada en este laboratorio. El calentador "casero" salió de un "rulo quemado" de los usados por algunos calefones. En la foto, el calentador "rulo" tiene cerca de $2\, \text{cm}$, y una resistencia eléctrica de aproximadamente $1,6\, \Omega$. En contraste, el calentador "original" tiene una resistencia que anda en el entorno de los $15\, \Omega$, lo que se traduce en una desventaja, al menos para el tipo de fuente voltaje de la que se dispone en este laboratorio, ya que resultó imposible "llevarla" a $2\, \text{A}$ (es parte de la practica). Notar ademas que: 1) los alambre de cobre están esmaltados (y trenzados dentro de un sorbete); 2) la espuma-plast fue cortada para que entre sin holgura en la boca del vaso Dewar del calorímetro, y se mantiene en su lugar con cinta adhesiva doble faz pegada contra la capa de corcho de la tapa y; 3) ademas del orificio centrado en la capa de espuma-plast, por donde "baja" el sorbete con los alambres de cobre trenzados, cerca de ese, es necesario un segundo orificio para el termómetro. Pero, ¿y dónde está el agitador? El propio calentador se usa de agitador: se sube y baja el sorbete estando el calentador sumergido en el agua. Para esta practica se necesitan $150\, \text{g}$ de agua, ni más ni menos para este calorímetro de boca ancha. Más agua es un problema para calentarla lo suficiente, como para variar de forma apreciable la temperatura. Por otro lado, si los $150\, \text{g}$ de agua se vierten directamente en en vaso Dewar, el nivel quedaría por debajo del punto más bajo del termómetro (digital, de los que se usan en cocina). Para solventar este problema, se hizo un vaso de aluminio a partir de una lata de refresco. La lata se cortó a $9\, \text{cm}$ de la base, resultando un vaso de $8\, \text{g}$. Este vaso de aluminio tiene la particularidad de que esta eléctricamente aislado: de fabrica a las latas de refrescos se las tratan químicamente con algún tipo de esmalte, para que el sabor metálico del aluminio no arruine el sabor original de la bebida, y de paso, esa capa transparente de esmalte sirve de aislante eléctrico. A su vez el vaso se eleva de altura, colocando un bloquesito de espuma-plast en la base del vaso Dewar, para que la punta del termómetro quede totalmente sumergida en el agua.

Esta practica se podría hacer como broche final en "5to", y por su puesto en "6to", pero sin embargo, la fundamentación teórica no tiene que ser la misma, pues en lo personal, "hilaría" más fino con "6to"
como una comprobación explícita del Primer Principio de la Termodinámica (dentro del calorímetro).

La fundamentación teórica de la practica: La energía cedida se corresponde con la energía eléctrica dada por la ley de Jolule, es decir:

Debido a la resistencia eléctrica del calentador, $R$, la energía eléctrica se transforma en energía calorífica absorbida por el agua (el calentador esta sumergido en $150\, \text{g}$ de agua), y el vaso de aluminio que la contiene, dada por la ecuación:

donde $c_{\text{agua}} = 4182\, \text{J/(kg}^{\circ}\text{C})$ y $m_{\text{agua}} = 0,150\, \text{kg}$ son respectivamente el calor específico y la masa del agua, y $c_{\text{alum}} = 897\, \text{J/(kg}^{\circ}\text{C})$ y $m_{\text{alum}} = 0,008\, \text{kg}$ lo correspondiente al vaso de aluminio.

Para no "torturar" algún cerebro adolescente, razonablemente se puede despreciar el termino correspondiente al vaso de aluminio, ya que se cumple:

o sea:

o dicho de otra forma: para incrementar la temperatura por igual en el agua y el vaso, para el agua se necesita $87$ veces más energía que para el aluminio, es decir, casi toda la energía calorífica es absorbida por el agua. Así, podemos continuar solo con el término correspondiente al agua (y omitir los subíndices):

De conservarse la energía dentro del calorímetro (pues la energía eléctrica se transforma en energía calorífica), y asumiendo que el calorímetro no tiene "fuga" de energía calorífica, debe cumplirse esta otra la igualdad:

es decir:

o reordenando términos:

Observar que la ecuación anterior, representa matemáticamente la conservación de la energía dentro del calorímetro, y al mismo tiempo, "una recta que pasa por el origen de coordenadas". Notar que las magnitudes entre paréntesis se pueden medir o averiguar, por lo que se reduce a una constante que se puede calcular fácilmente, y que "por suerte" para este experimento no es indispensable conocer su valor. Para tener una idea del valor de la constante, considerando los valores medidos en esta practica:

lo que conduce a:

Haciendo los cambios de variables convenientes:

se reduce a la susodicha ecuación de una recta por el origen (bien conocida por los estudiantes):

Hasta acá y con las debidas simplificaciones, "5to". Para la fundamentación teórica de "6to", el Primer Principio de la Termodinámica sería explicito, y básicamente establece qué: la variación de la energía interna de un sistema cerrado, $\Delta U$, puede ser consecuencia del calor, $Q$, absorbido y/o cedido por el sistema, o al trabajo, $$, realizado por y/o sobre el sistema, o en general, una combinación compleja de todo lo anterior: al sistema "entra" y "sale" energía al mismo tiempo como calor y trabajo. En el caso presente, el sistema cerrado sería el interior del calorímetro (agua + vaso + calentador + termómetro), y el ambiente la fuente de voltaje (y el resto del universo inmediato y no inmediato).

Haciendo la misma consideración que para "5to":

Para completar la ecuación surgirían dos posibilidades que conducen a los mismo:

• El aumento de la energía interna del sistema, sería consecuencia del calor ``desprendido'' por el calentador debido a su resistencia eléctrica ($\Delta U = Q_{\text{cedido al sist.}}$), siendo:
  
  

  ${\displaystyle Q_{\text{cedido al sist.}}=R·I^2·t\hspace{0.5em}\text{(ley de Joule)}}$



• El aumento de la energía interna del sistema, es consecuencia del trabajo realizado por las fuerzas eléctricas al desplazar cierta carga eléctrica por el calentador, cuando se establece una diferencia de
  potencial o voltaje entre sus extremos ($\Delta U = W_{\text{sobre el sist.}}$), siendo:
  
  

  ${\displaystyle W_{\text{sobre el sist.}}=q·\mathit{\Delta }V}$

  
  donde $q = I\cdot t$, y $\Delta V = R\cdot I$ (ley de Ohm).

Sea como sea, se llega al mismo balance de energía:

Para ilustrar lo antes dicho, aquí las medidas hechas por un subgrupo:

y la correspondiente grafica:

Observar en la grafica el valor del coeficiente angular de la recta de tendencia: $B = 0,722\cdots$ se "parece" al valor teórico de $0,751$ (nada mal para una practica de liceo).

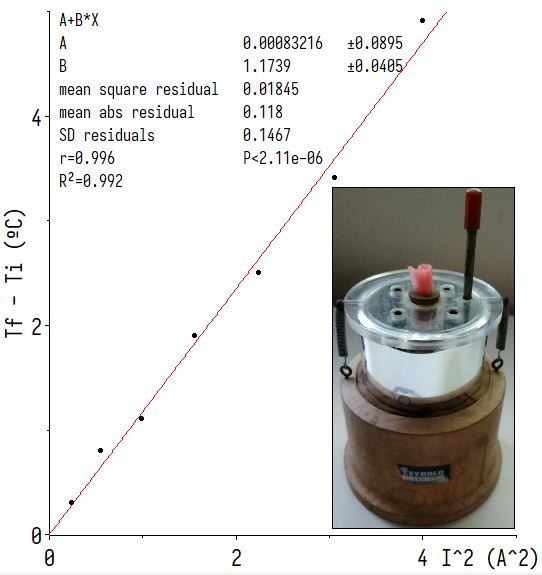
Por supuesto que todo esto se puede mejorar, y si se dispone de un calorímetro como éste (que lo hace todo mucho más fácil, y no se requiere de vaso), con los calentadores conectados en serie:

Las medidas hechas por otro subgrupo con este calorímetro (de "lujo"):

y la correspondiente grafica:

mucho mejor: pasa por el origen!!!